Дополнительные главы физики элементарных частиц (к.ф.-м.н., доц. В.В. Верещагин)

  1. Схема построения теории элементарных частиц (обзор основных идей)
    1. Пространство состояний. Эрмитовы операторы и наблюдаемые величины. Вероятность и условие полноты. Пуанкаре-инвариантность.
    2. Преобразования симметрии. Линейные (антилинейные) унитарные (антиунитарные) операторы; теорема Вигнера. Понятие группы и представления. Проективные представления. Алгебры, структурные константы, тождества Якоби, центральные заряды. Связные группы, группы Ли, абелевы группы.
    3. Группы Лоренца и Пуанкаре: генераторы и коммутационные соотношения. Операторы импульса, момента, буста. Одночастичные состояния, преобразовательные свойства и классификация. Отражения. Условия нормировки. Операторы рождения и уничтожения. Статистика Бозе -- Эйнштейна и Ферми -- Дирака.
    4. Структура произвольного оператора на пространстве состояний свободных частиц. Оператор числа частиц. Оператор импульса. Состояния "in" и "out". Оператор развития во времени, S-матрица.
    5. Принцип причинности и структура взаимодействий. Свободные поля. Заряды. Необходимость античастиц. Причинное поле, вычисление коммутатора. Дискретные преобразования и фазы. Причинные скалярное, векторное и спинорное поля. Поляризации.
  2. Теоретико-групповые методы
    1. Матрицы Паули и их свойства: коммутаторы, антикоммутаторы,
    2. произведения, следы. Формулы полноты. Символ 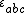\varepsilon_{abc}. Билинейные комбинации и свертка по индексам. Векторное произведение и формулы векторного анализа.
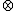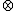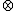    3. Группа вращений и классификация по моменту. Повышающие и понижающие операторы. Неприводимые представления. Разложение произведений 1/2\otimes1/2, 1/2\otimes1 и 1\otimes1 на неприводимые. Коэффициенты Клебша -- Гордана. Теорема Вигнера -- Эккарта. Спин-тензоры.
    4. Классические поля и теорема Нетер. Токи как генераторы группы симметрии. Вычисление скобок Пуассона (коммутаторов) вида [F(p),G(q)]_-. Многокомпонентные поля и преобразования внутренней симметрии. Линейные и нелинейные реализации симметрии.
    5. Изотопическая симметрия. Преобразование полей с I=1/2,1,3/2. Изоспиновая структура билинейных комбинаций и проекторы на "чистые" состояния. Изотопическая структура амплитуд пион-каонного и пион-пионного рассеяния.
    6. Киральная симметрия и группа SU_2 x SU_2. Линейные представления типа (\vec\pi,\vec\sigma) и (\vec\pi,\sigma). Нелинейное представление на \pi-мезонах; единственность с точностью до замены базиса. Закон преобразования производных и построение ковариантной производной пионного поля. Закон преобразования для произвольного поля (кроме пионного). Ковариантная производная для произвольного поля. Линейная и нелинейная сигма-модели.
    7. Абсолютно антисимметричный тензор 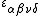\varepsilon_{\alpha\beta\nu\delta}; свертки по индексам. Запись определителя N-го ранга. Матрицы Дирака: определение, коммутаторы, антикоммутаторы, вычисление следов, разложение произведений. Операции с объектами типа 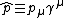\hat p \equiv p_\mu\gamma^\mu. Система базисных матриц и алгебра коммутаторов.
  3. Теоретико-полевые методы
    1. Т-экспонента и теорема Вика. Правила Фейнмана для теории 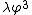\lambda\varphi^3. Древесная амплитуда для процесса 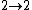2\to 2. Инвариантность S-матрицы относительно замены полевых переменных (на примере процесса 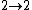2\to 2 в свободной теории вещественного скалярного поля).
    2. Переменные s, t, u и плоскость Мандельштама. Физические области каналов, кросс-симметрия. Теория 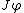J\varphi. Вычисление вероятности рождения N частиц в классическом поле. Распределение Пуассона и нормировка полной вероятности.
    3. Метод сокращенных проекторов для работы с изобарами.
  4. Расчеты амплитуд процессов рассеяния
    1. Древесные амплитуды процессов 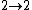2\to 2 в сигма-моделях; сечения рассеяния (полные и дифференциальные).
    2. Теория Юкавы (древесный уровень). Фермион-фермионное и фермион-антифермионное рассеяние. Приближение низких энергий и универсальность потенциала притяжения.
    3. Правила Фейнмана в квантовой электродинамике. Амплитуды рассеяния электрона на электроне и на позитроне. Низкоэнергетический предел и потенциал Кулона. Притяжение и отталкивание (знак пропагатора). Процесс рассеяния 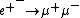e^+^-\to\mu^+\mu^-: амплитуда и сечение. Рождение пары кварк-антикварк и аннигиляция 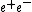e^+e^- в адроны.
    4. Пион-пионное рассеяние. Амплитуды с заданным изоспином в s- и t- каналах, определение длин рассеяния и параметров наклона. Кросс-симметрия и физические области на плоскости Мандельштама. Соотношение унитарности в области упругого рассеяния, унитарные ограничения для парциальных волн, фазы рассеяния. Унитарность в неупругой области. Древесная амплитуда в линейной и нелинейной сигма-моделях; длины рассеяния. Вклад 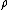\rho-мезона.
    5. Рассеяние пионов на нуклонах. Спиновая и изоспиновая структура амплитуды. Проекторы на состояния с разными изоспинами в s-, t- и u- каналах. Соотношение унитарности и разложение по парциальным волнам. Кросс-симметрия и физические области каналов. Формула для сечения рассеяния (неполяризованные нуклоны). Вершины 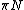\pi N-взаимодействия без производной и с производной, эквивалентность их на массовой поверхности нуклона. Расчет древесной амплитуды. Учет вклада изобары \triangle(1232). Длины рассеяния. Коэффициенты подпорогового разложения. Предел тяжелого нуклона. Длины рассеяния в линейной и нелинейной сигма-моделях.

 

Литература

  1. Л. Д. Ландау, Е. М. Лифшиц. Теоретическая физика. Т. 3: Квантовая механика. М., 1974.
  2. Л. Шифф. Квантовая механика. М., 1959.
  3. А. С. Давыдов. Квантовая механика. М., 1963.
  4. Дж. Тейлор. Теория рассеяния. М., 1975.
  5. П. А. М. Дирак. Принципы квантовой механики. М., 1979.
  6. А. И. Базь, Я. Б. Зельдович, А. М. Переломов. Рассеяние, реакции и распады в нерелятивистской квантовой механике. М., 1971.
  7. А. Мессиа. Квантовая механика. Тт. 1, 2. М., 1974.
  8. З. Флюгге. Задачи по квантовой механике. Тт. 1, 2. М., 1974.
  9. А. Камал. Задачи по физике элементарных частиц. М., 1968.
  10. H. Georgi. Lie algebras in particle physics. Benjamin/Cummings. Reading, MA. 1982.
  11. R. Gilmore. Lie groups, Lie algebras, and some of their applications. Wiley, New York, 1974.
  12. И. М. Гельфанд, Р. Л. Минлос, З. Я. Шапиро. Представления группы вращений и группы Лоренца. М., 1958.
  13. М. А. Наймарк. Линейные представления группы Лоренца. М., 1958.
  14. Ю. В. Новожилов. Введение в теорию элементарных частиц. М., 1972.
  15. Нгуен Ван Хьеу. Лекции по теории унитарной симметрии элементарных частиц. М., 1967.
  16. В. Д. Ляховский, А. А. Болохов. Группы симметрии и элементарные частицы. Л., 1983.
  17. Дж. Д. Бьеркен, С. Дрелл. Релятивистская квантовая теория. Тт. 1, 2. М., 1978.
  18. Н. Н. Боголюбов, Д. В. Ширков. Введение в теорию квантованных полей. М., 1976.
  19. Н. Н. Боголюбов, Д. В. Ширков. Квантовые поля. М., 1980.
  20. В. Б. Берестецкий, Е. М. Лифшиц, А. П. Питаевский. Теоретическая физика. Т. 4: Релятивистская квантовая теория. Ч. 1, 2. М., 1968.
  21. Д. В. Ширков, В. В. Серебряков, В. А. Мещеряков. Дисперсионные теории сильных взаимодействий при низких энергиях. М., 1967.
  22. Е. Бюклинг, К. Каянти. Кинематика элементарных частиц. М., 1975.
  23. С. Газиорович. Физика элементарных частиц. М., 1969.
  24. Т. Эриксон, В. Вайзе. Пионы и ядра. М., 1991.
  25. М. Б. Волошин, К. А. Тер-Мартиросян. Теория калибровочных взаимодействий элементарных частиц. М., 1984.
  26. В. Де Альфаро, С. Фубини, Г. Фурлан, К. Росетти. Токи в физике адронов. М., 1976.
  27. А. Н. Васильев. Функциональные методы в квантовой теории поля и статистике. Л., 1976.
  28. А. Н. Васильев. Квантовополевая ренормгруппа в теории критического поведения и стохастической динамике. СПб., 1998.
  29. А.А. Славнов, Л. Д. Фаддеев. Введение в квантовую теорию калибровочных полей. М., 1978.
  30. Дж. Тейлор. Калибровочные теории слабых взаимодействий. М., 1978.
  31. М. В. Андреев. Хромодинамика и жесткие процессы при высоких энергиях. М., 1981.
  32. П. Рамон. Теория поля. М., 1984.
  33. К. Хуанг. Кварки, лептоны и калибровочные поля. М., 1985.
  34. S. Coleman. Aspects of symmetry. Cambridge University Press. Cambridge, MA, 1985.
  35. J. F. Donoghue, E. Golowich, B. R. Holstein. Dynamics of the Standard Model. Cambridge University Press. Cambridge, MA, 1992.
  36. G. Sterman. An introduction to quantum field theory. Cambridge University Press. Cambridge, MA, 1993.
  37. M. Kaku. Quantum field theory. Oxford University Press, 1993.
  38. M. Peskin, D. Schroeder. Introduction to quantum field theory. Addison-Wesley. Reading, MA, 1995. S. Weinberg. The quantum theory of fields. vv. 1, 2, 3. Cambridge University Press. Cambridge, MA, 1999.
  39. S. Weinberg. Physica A, 96, 327 (1979).