Программа курса
- Термодинамическая гипотеза подобия вблизи критической точки.
- Ее обобщение для корреляционных функций. Критические размерности, соотношения между критическими показателями.
- Теория Ландау и классические критические индексы.
- Логарифмическая размерность. Классификация моделей теории поля по ренормируемости. Индекс расходимости для 1-неприводимой
корреляционной функции. Пример: модель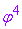
. - Неренормированное, ренормированное и базовое действие, контрчлены и связь между ними. Эквивалентность применения R-операции и добавления контрчленов. Локальность контрчленов.
- Размерная регуляризация. Вычисление интегралов в нецелой размерности. Формальный ответ и интерпретация как интеграл с вычитаниями. Примеры: Свертка степенных функций, преобразование Фурье от степени, степень от квадратичной по импульсам функции.
- Мультипликативная ренормировка. Вывод уравнения РГ для мультипликативно-ренормируемой модели.
- РГ-функции: бета-функция и аномальные размерности.
- Их выражение через константы ренормировки и общий вид в схеме MS.
- РГ-суммирование констант ренормировки. Связь инвариантных и затравочных зарядов. Особенности констант ренормировки в неподвижной точке. Решение уравнений РГ в терминах затравочных переменных.
- Решение уравнения РГ на примере парного коррелятора в модели 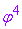при
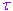>0. Инвариантные переменные. ИК-асимптотика инвариантных
переменных и коррелятора. Критический скейлинг и скейлинговая функция для коррелятора. - Обобщенная однородность и дифференциальные уравнения с постоянными коэффициентами. Каноническая масштабная инвариантность, канонические размерности для полей, параметров, связных и неприводимых корреляционных функций.
- Уравнение РГ в ИК-притягивающей неподвижной точке. Уравнение критического скейлинга. Критические размерности, их эпсилон-разложение.
- Решение уравнений РГ для модели 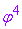при d=4 для парного коррелятора. Частные случаи 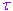=0 и
=0: логарифмические поправки
(или их отсутствие). - Суммирование вкладов типа g log(s) в модели 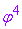при d=4 с помощью уравнений РГ.
- Уравнения РГ для производящих функционалов W и Г. Явное решение на примере Г.
- Классификация неподвижных точек уравнений РГ для однозарядной модели. ИК-асимптотика инвариантного заряда при наличии ИК-притягивающей неподвижной точки. Явные выражения в однопетлевом приближении.
- Определение ПР-подграфов. Операции L, R, R’. Операция К в схеме минимальных вычитаний. Определение операций R, R’ на подграфах и рекуррентное выражение контрчленной операции L через R’ и К.
- Переход к нормированным функциям Г и операции L_{a}. Дифференцирование по 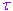. Переход к безмассовым диаграммам. Выражение для контрчленов через L(gamma).
- Вычисление диаграмм в координатном представлении при tau=0. Примеры расчета вклалов в Z для двухпетлевых диаграмм (No 4 или No 6 в таблице).
- Составные операторы. Производящие функционалы корреляционных функций с участием составных операторов. Канонические размерности
корреляционных функций с их участием. Новые ПР-графы; примеры для Ф^4. Ренормировка расширенной модели (с включением операторов). - УФ- конечный оператор, ренормированный оператор, операторные контрчлены. Классификация составных операторов по канонической размерности. Структура операторных контрчленов в схеме MS. Пример: структура контрчленов к операторам типа Ф^2, Ф^3, Ф^4 в модели Ф^4.
- Классификация составных операторов по канонической размерности. Ренормированный составной оператор. Матричная мультипликативная
ренормировка семейств операторов. Матрицы Q и Z. - Примеры явного расчета операторных контрчленов: оператор Ф^2 и тензорный оператор Ф\partial_{i}\partial_{j}Ф.
- Уравнение РГ для семейства операторов. Матрица аномальных размерностей. Критический скейлинг для семейств
операторов. Операторы с определенной размерностью. - Операторное разложение произведения полей на малых расстояниях. Свойства коэффициентных функций. Применение операторного разложения для нахождения ИК-асимптотики скейлинговой функции.
Экзамен
Дается 1 вопрос + задача.
Типичные задачи:
- вычислить безмассовую диаграмму в р-представлении (сведение к цепочкам и произведениям),
- написать R’ от диаграммы, т.е. найти все ПР-подграфы,
- вычислить L(диаграммы), т.е. ее контрчлен
