Программа курса

1. Феноменология развитой турбулентности. Инерционный, диссипационный и энергосодержащий интервалы. Внешний (интегральный) и внутренний (диссипационный) масштабы. Число Рейнольдса и автомодельность. Каскад энергии. Теория Колмогорова—Обухова.
2. Стохастическое уравнение Навье—Стокса для несжимаемой жидкости. Условие несжимаемости. Давление. Смысл случайной силы и выбор ее корреляционной функции.
3. Симметрии уравнения Навье—Стокса. Динамическое спонтанное нарушение симметрий при развитии турбулентности и их восстановление в режиме развитой турбулентности в статистическом смысле.
4. Квантово-полевая формулировка моделей критической динамики. Функционал действия, диаграммная техника и ее свойства.
5. ИК- и УФ-сингулярности диаграмм теории возмущений. Связь ИК- и УФ-проблем. Анализ УФ-расходимостей: общие принципы и особенности стохастической динамики. УФ-ренормировка. Уравнения РГ.
6. РГ-анализ стохастической гидродинамики.
7. Решение уравнений РГ. Инвариантные переменные. РГ-представления корреляционных функций.
8. ИК-скейлинг. Обоснование Второй гипотезы Колмогорова. Независимость корреляционных функций от вязкости.
9. Ренормировка составных операторов в стохастической гидродинамике. Использование функционаьных методов и галилеевой инвариантности для точного вычисления критических размерностей.
10. Перестановочность процедуры ренормировки и преобразования Галилея для составных операторов. Следствия галилеевой инвариантности для ренормировка составных операторов.
11. Операторное разложение Вильсона и проблема обоснования Первой гипотезы Колмогорова. Понятие опасных составных операторов.
12. Пример опасных операторов: операторы, построенные из поля скорости и его производных по времени любого порядка. Точный расчет их критических размерностей и суммирование их вкладов в операторноых разложениях. Эффекты переноса. Нарушение первой гипотезы Колмогорова для разновременных корреляторов.
13. Операторное разложение одновременного парного коррелятора. Особая роль галилеево-инвариантных скалярных составных операторов.
14. Критические размерности галилеево-инвариантных скалярных составных операторов.
15. Законы сохранения импульса и энергии. Точный расчет критических размерностей операторов скорости локальной диссипации, плотностей потока импульса и энергии и других операторов, входящих в законы сохранения.
16. Точное соотношение между скоростью локальной диссипации и коррелятором случайной силы.
17. Уравнение спектрального баланса энергии. Функция переноса, поток энергии по спектру. Гипотезы о свойствах функции переноса.
18. Проблема замыкания и EDQMN приближение для тройного коррелятора. Ренормгруппа, операторное разложение и асимптотики тройного коррелятора.
19. Решение уравнения спектрального баланса с помощью конформного преобразования. Колмогоровское решение с постоянным потоком энергии по спектру. Нулевые моды, неколмогоровские решения и обратный каскад энергии.
20. Использование ренормгруппы, операторного разложения и уравнения баланса энергии для вычисления константы Колмогорова.
21. Точный результат: закон 4/5 Колмогорова для структурной функции третьего порядка.
22. Об отклонениях от колмогоровского скейлинга для развитой турбулентности. Аномальный скейлинг и явление перемежаемости.
23. Феноменологические модели аномального скейлинга: log-нормальная модель, 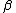-модель и мультифрактальные модели.
24. Турбулентный перенос пассивной скалярной примеси. Феноменологическая теория. Закон 4/3 Ричардсона для расплывания облака примесных частиц.
25. Ренормгруппа в задаче о турбулентной конвекции. Эффективное число Прандтля и обоснование закона Ричардсона.
26. Модель Обухова—Крейчнана для пассивной скалярной примеси, переносимой синтетическим полем скорости. Квантово-полевая формулировка, особенности диаграммной техники и РГ-анализ модели.
27. Опасные составные операторы и аномальный скейлинг в модели Обухова—Крейчнана. -разложение аномальных индексов.
28. Уравнеия Дайсона—Уайльда для корреляционных функций в модели Обухова—Крейчнана. Точное решение для парного коррелятора и функции отклика. Нулевые моды.
29. Обобщение модели Обухова—Крейчнана на случай сжимаемой жидкости. Ренормировка, операторное разложенеие. Аномальный скейлинг для парного коррелятора: -разложение.
30. Обобщение модели Обухова—Крейчнана на случай сжимаемой жидкости. Точное уравнение спектрального баланса энергии и его решения. Нулевые моды и нарушение Колмогоровского скейлинга для парного коррелятора. Фазовый переход к режиму с обратным каскадом энергии.
31. Точно-решаемые модели развитой турбулентности. Модель Гейзенберга для спектрального баланса энергии. Точное решение с помощью метода РГ. Точные результаты для 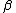-функции и неподвижной точки.
32. Гипотеза о локально изотропной турбулентности. Ее нарушение для задач переноса пассивной примеси. Асимметрия (skewness factor) и другие характеристики анизотропной турбулентности.
33. РГ-анализ модели Обухова—Крейчнана при наличии крупномасштабной анизотропии. Роль тензорных операторов в операторных разложениях. Расщепление уравнений для различных анизотропных секторов. Расчет главных индексов в старших анизотропных секторах.
34. Уточненная гипотеза о локально изотропной турбулентности. Иерархия критических размерностей, связанных с анизотропными секторами, как признак изотропизации развитой турбулентности. Рост старших нечетных моментов (hyperskewness и др.) в инерционном интервале как признак сохраняющейся анизотропной активности.
35. Совместное влияние анизотропии и сжимаемости на статистические свойства развитой турбулентности: случай пассивной примеси. Ослабление иерархии критических размерностей, связанных с анизотропными секторами, и усиление роста нечетных моментов.

Литература

1. Монин А.С., Яглом А.М. Статистическая гидромеханика, T.1,2. СПб, Гидрометеоиздат, 1996.
2. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М., Наука, 1986.
3. Васильев А.Н. Квантово-полевая ренормгруппа в теории критического поведения и стохастической динамике. СПб., Изд-во ПИЯФ, 1998.
4. Аджемян Л.Ц., Антонов Н.В., Васильев А.Н. Квантово-полевая ренормализационная группа в теории развитой турбулентности. УФН, 1996, т.166, N 12, с. 1257-1284.
5. Aджемян Л.Ц., Антонов Н.В., Васильев А.Н. Метод ренормализационной группы в теории развитой турбулентности. (Методическое пособие). Изд-во СПбУ, 1998.
6. U. Frisch. Turbulence: The Legacy of A.N.Kolmogorov. Cambridge University Press, Cambridge, 1995.
7. Orszag S.A. Fluid Dynamics, Les Houches, 1973. Ed. by R.Balian, J.-L.Peube. London, Gordon and Breach Publishing, 1977. P.235. (книга имеется в БАН).
8. McComb W.D. The Physics of Fluid Turbulence. Oxford, Clarendon, 1990.
9. Вильсон К., Когут Дж. Ренормализационная группа и epsilon-разложение. М., Мир, 1975.
10. Паташинский А.З., Покровский В.Л. Флуктуационная теория фазовых переходов. М., Наука, 1982.